Summary2

$O\sim T$

O 更好的isprime

时间限制：1500ms 内存限制：65536kb

通过率：399/418 (95.45%) 正确率：399/708 (56.36%)

题目描述

传统的判断素数的方式都是从 2 枚举到$ ⌊\sqrt{n}⌋$，试图寻找 $n$ 的因数，如果找不到则说明 $n$ 是素数。这种方法判断素数的时间复杂度是 $O(\sqrt{n})$，那我们能不能做的更好呢？

Miller-Rabin 素性测试，是一种基于二次探测定理和费马小定理的，用于快速测试一个奇数是否是素数的方法，对 $n$ 进行一次 Miller-Rabin 素性测试的时间复杂度仅为 $O(\log n)$。通过素性测试的数不一定是素数，可是没通过素性测试的数一定不是素数。用不同的数作为基底对 $n$ 进行多次素性测试，可以使得通过了这些素性测试的 $n$ 是素数的概率尽可能大。

不过对于范围 $[1,2^{32})$ 的数字，只要它能分别通过 $2,7,61$ 这三个数为基底的 Miller-Rabin 素性测试，它就一定是素数。

下面给出进行 Miller-Rabin 素性测试的代码，请你调用 Miller-Rabin 素性测试函数实现一个更好的 isprime 函数，并调用 isprime 函数完成本题要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
int qpow(int a, long long n, int mod) // 这只是一个快速幂，你可以不用管它
{
    int ans = 1;
    int base = a;
    while (n > 0)
    {
        if (n & 1)
        {
            ans = ans * (long long)base % mod;
        }
        base = (long long)base * base % mod;
        n >>= 1;
    }
    return ans;
}

/* 如果通过素性测试，那么下面这个函数返回1，否则返回0 */
int Miller_Rabin_check(int a, int n) // a是基底，n是你拿来进行素性测试的数
{
    int u = n - 1;
    while (u % 2 == 0)
    {
        u /= 2;
    }
    int v = qpow(a, u, n);
    if (v == 1)
        return 1;
    while (u <= n - 1)
    {
        if (v == n - 1)
            return 1;
        if (v == 1)
            return 0;
        v = 1ll * v * v % n;
        u *= 2;
    }
    return 0;
}
int isprime(int n)
{
    if (n == 2 || n == 7 || n == 61) // 作为基底的这三个数需要特殊处理
        return 1;
    /* 补全你的代码 */
}

输入

第一行一个正整数 t 表示数据组数，$1\le t\le 3\times 10^5$。

接下来 $t$ 行，每行一个正整数 $n$，$2\le n\le 10^9$。

输出

对于每组数据，如果 $n$ 是素数，输出 Yes，否则输出 No。

输入样例

1
2
3
4
5
6
7
6
2
61
47
1145
1919810
998244353

输出样例

1
2
3
4
5
6
Yes
Yes
Yes
No
No
Yes

Not Hint

如果你实在很闲可以看看原理

思路 没有思路，直接用and逻辑检测。唯一需要的是把代码框架写好：输入 --> 处理 --> 输出

P 解数织科学

时间限制：3000ms 内存限制：65536kb

通过率：7/20 (35.00%) 正确率：7/76 (9.21%)

题目描述

某咸鱼同学希望用若干数字描述行和列的涂色情况，如下图所示：

img

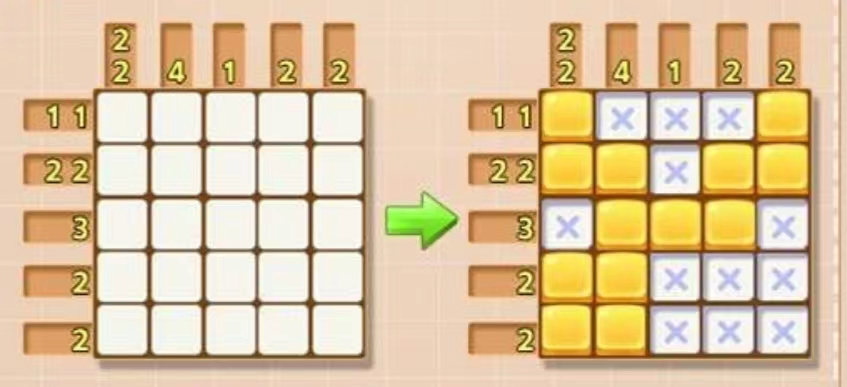
对于第一行，1 1表示有 $2$ 个长度为 $1$ 的 1（涂色）序列；对于第二列，4表示有 $1$ 个长度为 $4$ 的 1 （涂色）序列。

特别的，如果某行或某列没有一个涂色方块，我们用一个 0 表示。

请你根据给出的行列的情况，输出涂出颜色的地图。

输入

共 $2n+1$ 行。

第一行为一个正整数 $n$ 。

接下来 $n$ 行，输入从第一行到最后一行的情况，详见题目描述。

再接下来 $n$ 行，输入从第一列到最后一列的情况，详见题目描述。

保证 $n≤15$ ，且一定有解。

输出

$n$ 行，每行 $n$ 个字符（字符仅为 0 或 1），表示涂色后的地图。

本题采用 $\text{Special Judge}$ ，对于有多解的情况，请仅输出其中一种。

输入样例

1
2
3
4
5
6
7
8
9
10
11
5
1 1
2 2
3
2
2
2 2
4
1
2
2

输出样例

1
2
3
4
5
10001
11011
01110
11000
11000

Thinking

上网搜一下可以知道这还是一个比较要动脑的游戏，起源于国外，也可以搜到一些程序化解法——但是基本不可用，毕竟你从这些人写的博客就知道不仅技术水平低，同时文化水平也高不到哪里去。唯一比较好的一篇中文是数织游戏中的程序思维和数织的程序解法-CSDN博客，其中比较有趣的是对于数据结构状态的定义和一些个定理：

  • 网格每一格拥有三种状态
  • 定义连续空白条
  • 定义一个表示函数
  • 定理，平行传递性，交换不变形
  • ……

总的来说就是对现实问题进行数学抽象，建模简化，并进行程序化流程设计……当然，一般解决问题都是这样嘛。不过在思路受阻时宏观的考量的确能给人一些顿悟

还有一点就是，这个博客可能并不是原版，更多还待发掘。英文就有很多信息了[Solving Nonograms — Nonogram Solver (stevocity.me.uk)](https://stevocity.me.uk/nonogram/solve#:~:text=How to solve Nonograms yourself Before attempting to solve a)

数织 - 在线解谜游戏 (puzzle-nonograms.com)

原本自己想的是先确定行的数量，然后根据列的数量进行dfs暴力搜索——及时剪枝

Q 逞强好胜的 Yanami ！

时间限制：300ms 内存限制：65536kb

通过率：100/188 (53.19%) 正确率：100/721 (13.87%)

题目描述

$\text{Yanami}$ 想变得和 $\text{Alice}$ 一样强

但是现在她还无法做到，她只能研究 $\text{Alice}$ 留下的世纪难题

$\text{Alice}$ 给 $\text{Yanami}$ 留下了一个 “异或三角形”

一个 $n$ 层的异或三角形有以下特征：

  • 第 1 层有 1 个整数，第 2 层有 2 个整数，⋯⋯ ，第 $n$ 层有 $n$ 个整数
  • 如果用 $a(i,j)$ 表示异或三角形第 $i$ 层从左往右数的第 $j$ 个数 $(1≤j≤i) $，那么对于$ ∀1≤i≤n−1,1≤j≤i$，有 $a(i,j)=a(i+1,j)⊕a(i+1,j+1)$ ，即异或三角形中的每一个数等于其正下方相邻两个数的异或和

下方就是一个 $5$ 层的“异或三角形”：

1
2
3
4
5
4
  4  0
2  6   6
  3  1   7   1
1   2  3   4   5

对于第 4 层，从左往右有
$$
a(4,1)=a(5,1)⊕a(5,2)=1⊕2=3\

a(4,2)=a(5,2)⊕a(5,3)=2⊕3=1\

a(4,3)=a(5,3)⊕a(5,4)=3⊕4=7\

a(4,4)=a(5,4)⊕a(5,5)=4⊕5=1
$$

其他层类似

可以发现，只要确定了最底层的 $n$ 个数字，就可以推导出整个“异或三角形”

不幸的是，$\text{Alice}$ 给 $\text{Yanami}$ 留下的“异或三角形”，恰好只剩下最底层的 $n$ 个数字，其他数字都不见了

现在， $\text{Yanami}$ 想要知道“异或三角形”最顶层的那一个数字是什么，你能帮帮她吗？

输入

输入包括两行

第一行包括一个整数 $n$ ，表示“异或三角形”的层数

第二行包括 $n$ 个整数$ x_1,x_2,⋯,x_n$ ，表示“异或三角形”最底层的 $n$ 个数

输出

输出包括一行

第一行包括一个数，表示“异或三角形”最顶端的数值

输入样例 11

1
2
5
1 2 3 4 5

输出样例 11

1
4

输入样例 22

1
2
4
1 1 4 5

输出样例 22

1
1

样例解释

样例 2 的“异或三角形”如下：

1
2
3
4
      1
    5   4
  0   5   1
1   1   4   5

故答案为 1

数据范围

  • 对于 $35%$ 的数据，$1≤n≤10^3$
  • 对于 $100%$ 的数据，$1≤n≤10^5,0≤x_i≤10^9$

题目背景

没错！

一次又一次地 屡败屡战！

是眼泪教会我坚强

我相信

总有一天 总有一天 会迎来美满结局

开始转动吧！无与伦比的命运

——《逞强好胜的女孩》

img

思路 这道题在数量比较小的时候规律还是非常好找的，可以省略中间众多的异或过程，直接计算出需要哪些元素作异或操作就可以。具体方法是从1开始右移一格得到新向量，与原先向量作异或和，n次迭代后得到为1的分量即为需要做异或和操作的元素，否则舍弃。因为计算机中是二进制，所以可以根据二进制表示的周期性来对迭代过程进行加速。但是这题尝试好久都没有得到有效解决，可能是规律找错了。 大概有100人通过了，心理挺着急的，为什么别人都会，就我不会？想不出来，前后浪费半天——悲

R 摩卡与主唱

时间限制：1000ms 内存限制：65536kb

通过率：107/193 (55.44%) 正确率：107/742 (14.42%)

题目描述

作为乐队的主唱，Ykn 和 Ran 对音乐有着不同的理解。

Ykn 在听一首音乐时，会格外关注音乐中高音转低音的部分；Ran 在听一首音乐时，会格外关注音乐中低音转高音的部分。在听完一次演唱会后，二人对其中的一首曲子格外感兴趣，经过讨论后，二人发现这首曲子所有音符只由高音和低音组成，且其中的高音转低音次数和低音转高音次数是完全相同的。但是二人只能回忆起其中的部分音符。

为了能还原这首曲子，Ykn 和 Ran 找到了会编程的 Moca。

输入

第一行一个正整数 $n$ ，表示曲子音符的个数，$1≤n≤100000$ 。

第二行 $n$ 个字符，表示 $n$ 个音符，每个音符只有 $1\ 0\ ?$ 三种可能的输入，分别表示这个音符是高音音符，低音音符以及回忆不起来的音符。

输出

输出 1 行，代表原曲有多少种可能（由于两个人的记忆可能存在偏差，所以结果为 0 也是有可能的），由于结果可能很大，你需要将正确的答案对 $10^9+7$ 取模后输出。

输入样例

1
2
5
1?001

输出样例

1
2

THINK

无

样例解释

若想符合条件，原曲有 $11001$ 和 $10001$ 两种可能。

Author：Moca

该题也是，别人都会，为什么就我不会——懊恼。

应该是一个能在线性时间处理的问题，不然不会有这种数据。所以，处理的时候应该只需要考虑局部就行，最后验证可行性

Moca是种$Italian$浓缩咖啡:coffee:,还有拿铁，记得大川课上还让我们每次做咖啡给他品，居然把这个忘了……

S 哈希攻击

时间限制：2000ms 内存限制：65536kb

通过率：18/42 (42.86%) 正确率：18/147 (12.24%)

题目描述

字符串以某种方式映射到整数上的过程，称作「字符串哈希」。由这个字符串经过哈希得到的整数，我们称其为字符串的「哈希值」。以下是一种比较常用的字符串哈希公式：

$f(s)=(∑_{i=1}^n a_i×b^n−i)\mod p$

其中，$a_i$ 是字符串第 $i$ 位对应字符所需要映射的值，$b$ 是小于 $p$ 的正整数，$p$ 是一个大质数。

当两个字符串完全相同时，它们的哈希值也必定完全相同。可是反之，当两个字符串的哈希值完全相同时，它们本身并不一定会完全相同。因为哈希函数最终对 $p$ 取模的操作，使得无穷无尽的字符串最终只能被映射到 $0∼p−1$ 的正整数上，而这就必定要产生多个不同字符串拥有同一哈希值的情况。这种两个不同的字符串具有相同的哈希值的情况，我们称其为「哈希冲突」

可是 Gino 并不害怕。他使用如下函数对字符串进行哈希，并且认为你无论如何也无法在短时间内产生无穷多的字符串，并从无穷多的字符串中找到哈希冲突的情况。

1
2
3
4
5
6
7
8
9
int strhash(char s[], int len, int b, int p)
{
    int val = 0;
    for (int i = 0; i < len; i++)
    {
        val = (1ll * val * b + s[i] - 'a' + 1) % p;
    }
    return val;
}

请你找到任意两个字符串，使它们满足以下条件：

  • 仅由小写字母 a-z 组成
  • 两者长度相同，且长度 $n$ 满足 $1≤n≤104$
  • 两者不完全相同，却在给定 $b,p$ 的条件下有着一致的哈希值

输入

两个由空格隔开的正整数 $b,p$，含义与题意相同。

  • 对于 10%的数据，31≤b<p≤1009
  • 对于 30% 的数据，31≤b<p≤1000033
  • 对于 100% 的数据，31≤b<p≤1000000007

所有数据均保证 p 是一个质数。

输出

两行，分别输出你找到的两个字符串，需要满足题目给出的条件。满足条件的字符串有很多组，你只需要输出任意一组即可。

输入样例

1
131 1033

输出样例（答案不唯一）

1
2
vda
ciu

样例解释

对于字符串 vdl，其哈希值为 $(22×1312+4×1311+1×1310)\mod 1033=378067\mod 1033=1022$

对于字符串 ciu，其哈希值为 $(3×1312+9×1311+10×1310)\mod 1033=52672\mod 1033=1022$

两个不同的字符串却有着同样的哈希值，因此这组输出是正确的。

注意你的输出不必和输出样例相同，只需满足题目条件即可。

$HASHHACKER$: Codeforces Rating of @cwz2024

THINK

有点思路。解法一定跟生日问题有关。

可以思考这个哈希函数的计算式，二者相减可以得到一个多项式，而系数正好就是一个$b$ 进制数，但是要求是 ASCll 码中的小写字符，所以需要转化成一个系数相差不超过26的$b$进制

问题成功转化

T 多重哈希攻击

时间限制：2000ms 内存限制：65536kb

通过率：11/22 (50.00%) 正确率：11/114 (9.65%)

本题是题目《哈希攻击》的困难版本。

题目描述

在 $\mathscr{HASHHACKER}$ 的攻击下，Gino 自认为没有破绽的字符串哈希被攻破了！可是 Gino 并不打算放弃。于是，他找到了一种叫「多重哈希」的技术。

我们知道，字符串可以通过以下方式映射到一个整数上：
$$
f(s)=(∑_{i=1}^n a_i×b^n−i)\mod p
$$
其中，$a_i$ 是字符串第 $i$ 位对应字符所需要映射的值，$b$ 是小于 $p$ 的正整数，$p$ 是一个大质数。

而「多重哈希」，会使用两组及以上的 $b,p$ 将字符串同时映射到两个及以上的整数上，以大大降低哈希冲突的概率。

Gino 使用的哈希函数与之前一样：

1
2
3
4
5
6
7
8
9
int strhash(char s[], int len, int b, int p)
{
    int val = 0;
    for (int i = 0; i < len; i++)
    {
        val = (1ll * val * b + s[i] - 'a' + 1) % p;
    }
    return val;
}

不同的是，他这次决定使用两组不相同的 $b,p$ 进行哈希。

请你找到任意两个字符串，使它们满足以下条件：

  • 仅由小写字母 a-z 组成
  • 两者长度相同，且长度 n 满足 $1≤n≤104$
  • 两者不完全相同，却在给定的两组 $b,p$ 的条件下都有着一致的哈希值

输入

共两行，每行两个由空格隔开的正整数 b,p，含义与题意相同。

  • 对于 $30%$ 的数据，$31≤b<p≤33331$
  • 对于 $100%$ 的数据，$31≤b<p≤1000000007$

所有数据均保证 $p$ 是一个质数。

所有数据均保证 $b_1≠b_2$ 与 $p_1≠p_2$ 至少有一个成立

输出

两行，分别输出你找到的两个字符串，需要满足题目给出的条件。满足条件的字符串有很多组，你只需要输出任意一组即可。

输入样例

1
2
31 1009
114 1033

输出样例（答案不唯一）

1
2
rkfmftoxsjtoxsjrkfmfrkfmftoxsjrkfmfrkfmfrkfmftoxsj
toxsjtoxsjtoxsjtoxsjrkfmftoxsjrkfmftoxsjrkfmfrkfmf

样例解释

$b=31,p=1009$ 的情况下，两字符串的哈希值都为 $0$。

$b=114,p=1033$ 的情况下，两字符串的哈希值都为 $1$。

Hint

为了降低思考难度，本题的输出样例极其富有启发性。

对于随机数生成函数 rand 来说，请注意，它的随机性有可能在你的本地运行环境下的表现并不好。

在出题者的本地环境下，RAND_MAX:$ 32767$，即 $2^{15}-1$

  • 二进制表示下，生成的随机数的最低位的循环节：$2^{17}$
  • 二进制表示下，生成的随机数的次低位的循环节：$2^{18}$
  • 二进制表示下，生成的随机数的第三低位的循环节：$2^{19}$

也许可以解答你在本地调试时遇到的 “灵异事件”。

注 这题真是不会了，毕竟和密码相关邻域很紧密。之前学CTF的时候连进门都算不上，这里看不懂也难怪

同样是哈希攻击，但是最近 bing 的搜索结果却不太好，浏览器还是要学一学搜索语法才行。而且对于专业邻域的知识，当然是要到专家数据库中搜索，而不是在一般互联网的垃圾堆中浪费时间和生命

#I 💖 [PUAA]
Summary2
http://example.com/2024/10/09/Summary2/
作者
独步星尘
发布于
2024年10月9日
许可协议