Summary1

$H\sim N$

H 吉他与孤独与蓝色星球！

时间限制：500ms 内存限制：65536kb

通过率：241/497 (48.49%) 正确率：241/1899 (12.69%)

题目描述

长大以后，$\text{Hitori}$ 成为了远近闻名的社交达人！

$\text{Hitori}$ 一共交到了 $m$ 个朋友，每个朋友都有一种独一无二的颜色。为了方便，我们用数字来表示每位朋友的颜色，即：第 $i$ 位朋友的颜色为 $i$ 。

这一天，$\text{Hitori}$ 又在坐地铁。她发现线路图上从左到右一共有 $n$ 个换乘站，第 $i$ 个换乘站对应的线路颜色为 $a_i$$a_i$ ，并且 $1≤a_i≤m$ 。对于这样一个由颜色构成的序列， $\text{Hitori}$ 将其称为整数序列 $a$ 。

$\text{Hitori}$ 想起了她的 $m$ 个朋友，她想知道，在序列 $a$ 中，有多少个长度为 $m$ 的子段，满足在子段中，每位朋友的颜色都恰好只出现了一次。

说明： 一个序列是 $a$ 的子段，当且仅当该序列由若干个 $a$ 中连续的元素按顺序组成。如，$[1,2,3]$ 和$ [3,3,5]$ 是 $[1,2,3,3,5]$ 的子段，但 $[1,3,5]$ 和 $ [1,3,2]$ 不是。

输入

输入包含两行。

第一行包含两个整数 $n,m$ ，分别表示序列 $a$ 的长度和 $\text{Hitori}$ 朋友的数量。

第二行包含 $n$ 个整数 $a_1,a_2,a_3,⋯,a_n (1≤a_i≤m)$，表示颜色序列 $a$ 。

输出

输出一行，包括一个整数，表示满足要求的子段数量。

输入样例 1

5 3
3 2 1 3 1

输出样例 1

2

输入样例 2

5 4
3 2 1 4 3

输出样例 2

2

输入样例 3

2 3
3 1

输出样例 3

0

样例解释

在样例 $1$ 中，长度为 $3$ 的子段有 3 个，分别是 $[3,2,1],[2,1,3],[1,3,1]$ 。

其中 $[3,2,1],[2,1,3]$ 满足 $3$ 种颜色都恰好出现了一次。

$[1,3,1]$ 中，$2$ 没有出现，$1$ 出现了两次，不符合条件。

故答案为 $2$ 。

数据范围

• 对于 $88%$ 的数据，满足 $1≤n,m≤5000$
• 对于 $100%$ 的数据，满足 $1≤n,m≤10^6$

题目背景

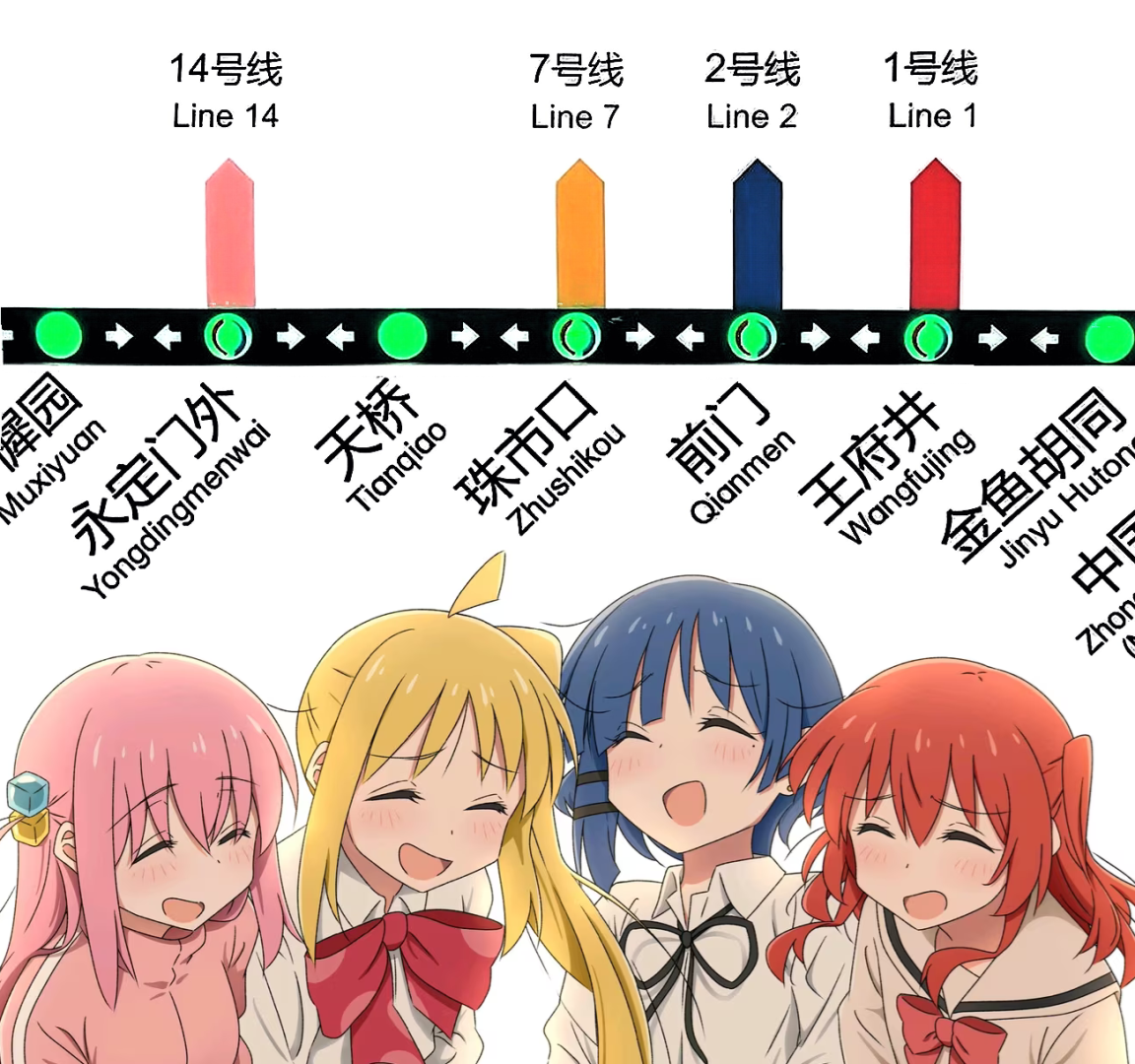
在北京地铁 88 号线上，$\text{Hitori}$ 发现线路图上 $14$ 号线、$7$ 号线、$2$ 号线和 $1$ 号线的颜色依次是粉色、黄色、蓝色、红色，正好对应了她和她的三个朋友。

只不过为什么粉色要离得比较远呢？

$Hitori$ 不由得唱起了：

愚昧无知的我唯有放声高歌

倾诉一切吧 对那星辰

——《吉他与孤独与蓝色星球》

思路

滑动区间(考察前后两个指针)，并且同时对元素状态和数量储存判断。这种思想有很多算法都有，比如说KMP算法等，可以将时间复杂度降低到线性。仔细想一下，其实如果单独对每一个区间都去计数，前后两个需要计算的区间有很大一部分是重叠的，也就是说这样会有很大的重复计算——能否通过复用之前的数据成了高效解决问题的一种思路

I Hide an integer

时间限制：1000ms 内存限制：65536kb

通过率：408/452 (90.27%) 正确率：408/1179 (34.61%)

题目背景

Koishi 想要用平衡五进制加密一封书信，传递给 Kisin Remilia。

题目描述

所谓平衡五进制，是一种计数方法，在这个计数方法中， 从低到高第 $i$ 位的权重为 $5^i$，而第 $i$ 位只可能是 $−2,−1,0,1,2$ 五种（而非一般五进制中的 $0,1,2,3,4$）。为了表示方便，我们记 $−1$ 为 $A$，$−2$ 为 $B$。

比如，对于一个平衡五进制数 $1AB$，其值相当于十进制下的 $1×52+(−1)×51+(−2)×50=18$。

具体到书信来说，这封书信一共有 $T$ 个单词，每个单词可以表示为一个自然数 $n$。为了加密这个自然数，Koishi决定用平衡五进制的方式重新书写每个数字。现在给定这个书信的每个原始单词，需要你输出加密后的书信。

输入

第一行一个正整数 $T\ (1≤T≤105)$，表示书信里的单词总数。

接下来 $T$ 行，每行一行一个自然数 $n$（$0≤n≤109$），表示书信里的单词。

输出

对于每个单词，输出一行一个平衡五进制数，表示该单词加密后的结果。

需要注意的是，你的输出不应该包含多余的前导零。

输入样例

9
72
121
97
99
105
110
116
104
0

输出样例

1BA2
10A1
1AA2
1A0A
1A10
1A20
10B1
1A1A
0

提示

Koishi：如果想不出如何直接转化，不如先想想如何把一个十进制数转化成一个一般的五进制数，再想想一般五进制和平衡五进制的关系？

以及，输入本身是 8 个字母。

THINK

注意提示

J 神奇的传送门

时间限制：1000ms 内存限制：65536kb

通过率：186/252 (73.81%) 正确率：186/713 (26.09%)

题目描述

Zeta
和他的朋友们正在探索一组神奇的传送门。经过不懈的探索，他们发现，每穿过一次传送门，自己都会被传送到某个传送门的门前（可能是同一扇门）。

如果有 $n$个人分别站在 $n$ 扇门前，每当他们同时穿过自己面前的门时，他们就会分别被传送到不同门前，即每扇门前有且仅有一人。

传送门之间有一定的传递关系，我们可以用一个数列 ${a_n}$ 来表示某一次的传递关系，$a_i$ 表示 $i$ 号 送到 $a_i$ 号门，显然，每一次传送中传送门的传递关系一般是不同的。

现在有 $n$ 个人分别站在 $n$ 个传送门前，人和传送门的编号均为 $1,2,…,n$ ，起初他们站在自己对应的传送门前，他们会共同穿过 $k+1$ 次自己面前的传送门，已知他们的最终位置，以及从倒数第 $2$ 次传送到第 $1$ 次传送中传送门的传递关系，请你推断出最后一次传送中传送门的传递关系。

一句话概括：对于集合 $A={1,2,…,n}$ 存在 $n!$ 种双射（一一映射）$f:A→A$ , 现给出其中 $k+1$ 种映射 $f,f_k,f_{k−1},…,f_2,f_1$ , 求映射$f_{k+1}$ 使得 $f_{k+1}∘f_k∘…∘f_2∘f_1=f$ .（其中 ∘ 为映射的复合，例如 $(f1∘f2)(x)=f1[f2(x)]$ 。）

输入

第一行 1个整数 t 表示数据组数。($1≤t≤50$)

对于每组数据输入 $k+2$ 行：

第一行 2 个整数 $n,k$ 含义如题所示。（$1≤n≤2×103,1≤k≤100$）

第二行 $n$ 个整数，第 i 个数表示第 i 号人最终站在的传送门的编号。

接下来 k 行，每行 $n$ 个整数，从后往前地给出传送门的传递关系，即第 m 行第 i 个数 $a_i$ 表示在倒数第 m 次传送中，i号门传送到 $a_i$ 号门。

输出

输出共 t 行。

对于每组数据，输出一行 n 个整数，第 i 个数 $a_i$ 表示在最后一次传送中 i 号门传送到 $a_i$ 号门。

输入样例

1
5 3
2 1 3 4 5
1 5 3 2 4
4 1 3 2 5
5 1 2 4 3

输出样例

3 1 5 2 4

样例解释

起初，$1,2,3,4,5$ 号人分别在 $1,2,3,4,5 $号门前。

然后，经过输入样例最后一行 5 1 2 4 3 的传送，$1,2,3,4,5$ 号人分别在 $5,1,2,4,3$ 号门前。

然后，经过 4 1 3 2 5 的传送，处在 $1$ 号门前的 $2$ 号人被传送到 $4$ 号门前，以此类推，$1,2,3,4,5$
号人分别在 $5,4,1,2,3$ 号门前

然后，经过 1 5 3 2 4 的传送，$1,2,3,4,5$ 号人分别在 $4,2,1,5,3$ 号门前

最后，经过输出样例 3 1 5 2 4 的传送，处在 $4$ 号门的 $1$ 号人被传送到 $2$ 号门前，以此类推，$1,2,3,4,5$ 号人分别在 $2,1,3,4,5$ 号门前，符合输入样例第三行。

THINK

函数就是特殊的关系，关系就是有序偶，有序偶可以用矩阵形式表示。所以就按照函数复合来实施矩阵运算就行——难点在于别写错，写错了重写一遍吧，debug可能浪费更多时间

K L形瓷砖

时间限制：1000ms 内存限制：65536kb

通过率：47/86 (54.65%) 正确率：47/301 (15.61%)

题目描述

你是一个装修公司的CEO，今天你接到了一单生意，让你在月球上贴瓷砖，客户给出的价格不菲，并且愿意承担来往的费用，你很心动，但是客户提出了一些要求，你的任务是给出满足客户要求的方案。

客户主要的要求如下：

• 只能使用如下的瓷砖（不可旋转）

  

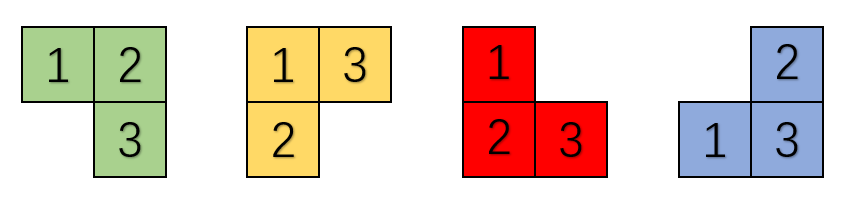
• 要布满一个边长为 $n$ 的正方形区域，除了其中一个用来放置人类月球纪念碑的位置。

方案有多种，输出其中一种即可

输入

第一行为一个整数 $n$ ，含义如上，保证： $n=2^k,0≤k≤10$。

接下来两个整数，表示人类月球纪念碑的坐标 (从 $0$ 开始，左上角为坐标原点，$x$ 表示行号，$y$ 表示列号)。

输出

$\frac{n^2-1}{3}$ 行，每行一个字母，三个坐标，表示一块瓷砖，字母表示颜色，坐标是该瓷砖 $3$ 个部分的坐标，按照上图标号的顺序输出。

如果不存在可行的方案，请输出 None 。

瓷砖的输出顺序随意。

输入样例1

2
1 0

输出样例1

g (0,0) (0,1) (1,1)

输入样例2

4
1 1

输出样例2

y (0,0) (1,0) (0,1)
r (2,0) (3,0) (3,1)
g (0,2) (0,3) (1,3)
b (2,1) (1,2) (2,2)
b (3,2) (2,3) (3,3)

样例解释

对于样例 11：黑色的圆表示纪念碑

对于样例 22：

Author: YUKI

THINK

砖人

注意：自己多画两个图出来观察划分方法——明白整个过程怎么样划分子区域就能很好明白。

结果是一个 $4*4$ 的递归分治，但是类型比较多，所以要注意代码组织。

L NEVER FORGET

时间限制：1000ms 内存限制：65536kb

通过率：41/135 (30.37%) 正确率：41/494 (8.30%)

题目描述

• Hitori 发现了 $n$ 个正整数 $a_1,a_2,⋯,a_n$，它们构成了一个可重集合 $S$ ，即 $S={a_1,a_2,⋯,a_n}$，且 $∀a_i\in S, 1\le a_i\le n$ 。
• Nijika 取出了 $S$ 的所有非空子集，并告诉你，每个非空子集的价值等于该子集中所有元素的和，即对于 $T⊆S (T\neq \varnothing )$ ，其价值 $V_T=\sum_{a_x\in T}a_x$ 。
• $\text{Ryo}$ 将 $S$ 所有非空子集的价值从小到大排序，排序后的价值构成了序列 $w_1,w_2,⋯,w_{2^n−1}$ 。
• $\text{Ikuyo}$ 想问你，$w_{2^n-1}$ 等于多少？

输入

输入包括两行

第一行包括一个正整数 $n$

第二行包括 $n$ 个正整数 $a_1,a_2,⋯,a_n$

输出

输出包括一行

第一行包括一个正整数 $w_{2^n -1}$

输入样例

3
2 1 2

输出样例

3

样例解释

$S$ 的所有非空子集分别为 ${2},{1},{2},{2,1},{2,2},{1,2},{2,1,2}$ 。

价值分别为 $2,1,2,3,4,3,5$ 。

从小到大排序后为 $1,2,2,3,3,4,5$ 。

故 $w_{2^n -1}=w_4=3$ 。

数据范围

• 对于 $50%$ 的数据， $1≤n≤16$
• 对于 $70%$ 的数据， $1≤n≤200$
• 对于 $100%$ 的数据， $1≤n≤500, 1≤a_i≤n$

题目背景 - 续

等着你的我

我在等着你

连无尽的明天

都能够穿过

停下脚步 回头看

叹息着无休止的今天

永远这种事 记忆什么的

明知道这些都是留存不下来的

我还是为此苦恼挠头

在心的角落里哭泣

想要请你记住那些

在高架桥下渡过的美好时光

我依然在后悔 有话没能说出口

落荒而逃的那天

我们手牵手

曾经那些难舍难分的感情

这就是我的一切了

但是连这些 现在都失去了

时过境迁 物是人非

明知道世事无常

我却依然苦恼地直挠头

悔恨着有话说不出口的今天

想要请你记住那些

在高架桥下渡过的美好时光

我依然在后悔 有话没能说出口 落荒而逃的那天

等着你的我

我在等着你

连无尽的明天都能够穿过

我今天也依然苦恼地挠头

一直在黯然伤心

我非你莫属

——《Re:Re:》

思路

这题真不会，别人的思路是一个$n^3$的dp和一个前缀和与二分——但是没听懂。还有一个思路是幂集的和是对称的，这样就可以缩小枚举区间，找出答案了

M 好想变得和你一样强！！！

时间限制：1000ms 内存限制：65536kb

通过率：97/172 (56.40%) 正确率：97/488 (19.88%)

题目背景

所以，海的那边是什么？

题目描述

曾经，有一位强者名叫 Alice ，$\text{\text{Chtholly}}$ 想变得和她一样强

但是 $\text{\text{Chtholly}}$ 现在还无法做到，她只能摆弄手中的 $n$ 个整数 $a_1,a_2,⋯,a_n$

$\text{\text{Chtholly}}$ 可以进行若干次操作，每次操作可以从 $n$ 个整数中任意选择一个数 $ai$ ，将它加 1 或减 1

一个整数序列被称为“好序列”，当且仅当其单调递增，且相邻两数的差值为 11

如 $[2,3,4]$ 和 [9,10,11,12][9,10,11,12] 是“好序列”，而 [1,1,4,5][1,1,4,5] 和 [1,3,4][1,3,4] 不是“好序列”

$\text{\text{Chtholly}}$ 想知道，最少通过多少次操作，可以将序列 $a_1,a_2,⋯,a_n$ 变为“好序列”

输入

输入包括两行

第一行包括一个整数 $n$

第二行包括 $n$ 个整数，$a_1,a_2,⋯,a_n$

输出

输出包括一行

第一行包括一个整数，表示最少的操作次数

输入样例 1

4
7 1 4 9

输出样例 1

11

输入样例 2

7
1 9 1 9 8 1 0

输出样例 2

29

样例解释

对于样例 1 ，最优解之一是使序列变为 [2,3,4,5][2,3,4,5]

数据范围

• 对于 $50%$ 的数据，$1≤n≤103$
• 对于 $100%$ 的数据，$1≤n≤105,0≤a_i≤109$

Hint

本题可能需要用到排序算法 ，以下代码可以实现对数组的高效排序（从小到大），平均时间复杂度为 $O(n\log 2n)$，可供参考

（课堂上没有讲解排序之前可以先不懂原理，能够把以下代码合理地嵌入进自己的程序之中来实现排序即可）

#include <stdio.h>
#include <stdlib.h> //头文件需要添加 stdlib.h
int cmp(const void *p1, const void *p2) {
	if (*((int*)p1) <= *((int*)p2))
		return -1;
	return 1;
}
int a[10] = {1, 9, 4, 9, 2, 0, 2, 3}; //此处元素下标从 0 开始
int main() {
	int n = 8; // n 为数组中的元素个数
	qsort(a, n, sizeof(a[0]), cmp); // 排序
	for (int i = 0; i < n; i++)
		printf("%d ", a[i]);
	printf("\n");
	return 0;
}

本题可能需要用到 long long ，请留意

题目背景 - 续

屏幕在深夜微微发亮

思想在那虚树路径上彷徨

平面的向量交错生长

织成 忧伤的网

剪枝剪去我们的疯狂

SPFA告诉我前途在何方

01背包装下了忧伤

笑颜 洋溢脸庞

键盘微凉 鼠标微凉

指尖流淌 代码千行

凸包周长 直径多长

一进考场 全都忘光

你在OJ上提交了千百遍

却依然不能卡进那时限

双手敲尽代码也敲尽岁月

只有我一人 写的题解

凋零在OJ里面

tarjan陪伴强联通分量

生成树完成后思路才闪光

欧拉跑过的七桥古塘

让你 心驰神往

队列进出图上的方向

线段树区间修改求出总量

可持久留下的迹象

我们 俯身欣赏

数论算法 图论算法

高斯费马 树上开花

线性规划 动态规划

时间爆炸 如何优化

我在OI中辗转了千百天

却不让我看AK最后一眼

我用空间换回超限的时间

随重新编译 测完样例

才发现漏洞满篇

原来CE 是因选错语言

其实爆0 只因忘写文件

如果标算太难请坚定信念

不如回头再看一眼题面

以那暴力模拟向正解吊唁

蒟蒻的蜕变 神犇出现

终将与Au擦肩

屏幕在深夜微微发亮

我心在考场

—— Menci/24OI 《膜你抄》

THINK

假设最终所得的序列为$k,k+1,…,k+n-1$,则目的可以转化成求函数$f(k)=\sum_{i=0}^{n-1}|k+i-a_i|=\sum_{i=0}^{n-1}|k-(a_i-i)|$ 的最小值，这是一个一维绝对值函数，中学数学告诉你最值点在序列 $a_i-i$ 的中位数上，所以先排序，然后求中位数，最后计算答案即可

N 世界上最幸福的女孩

时间限制：1000ms 内存限制：65536kb

通过率：279/366 (76.23%) 正确率：279/1368 (20.39%)

题目背景

所以，我敢肯定……现在的我……不管别人怎么说，一定是世界上最幸福的女孩。

$\mathbf{Chtholly⋅Nota⋅Seniorious}$

题目描述

$\text{Chtholly}$ 收到了一份生日礼物

生日礼物里有 $n$ 个整数 $x_1,x_2,⋯,x_n$，$\text{Chtholly}$ 可以随意指定每一个整数的数值，但是要满足：对于任意的 $1≤i≤n$ ，都有 $1≤x_i≤m$，且 $x_i$ 互不相等

$\text{Chtholly}$ 不喜欢三角形，所以她不希望这 $n$ 个整数中存在三个数，可以作为同一个三角形三条边的边长，即：不存在$ x_i,x_j,x_k$（$1≤i,j,k≤n$, 且 $i,j,k$ 互不相等），满足 $x_i+x_j>x_k$

$\text{Chtholly}$ 想知道，是否存在一种对于 $x_1,x_2,⋯,x_n$ 的数值指定方案，满足：对于其中的任意三个数，都不能作为同一个三角形三条边的边长

输入

输入包含多组数据

第一行包含一个整数 $T$ ，表示数据组数

接下来 $T$ 行，每一行包含两个整数 $n,m$ ，表示一组数据

输出

对于每组数据，输出一行

若存在满足条件的方案，则输出 YE5，否则输出 N0

输入样例

7
10 2
4 7
5 7
3 3
114 514
1 1
16454536251 1145141919810

输出样例

N0
YE5
N0
YE5
N0
YE5
N0

样例解释

• 当 $n=4,m=7$ 时，可以使 4 个整数分别为 $1,2,4,7$ ，满足要求
• 当 $n=3,m=3$ 时，可以使 3 个整数分别为 $1,2,3$ ，满足要求
• 当$ n=1,m=1$ 时，显然满足要求

数据范围

• 对于 $100%$ 的数据，满足 $1≤T≤10^5,1≤n≤10^{18},1≤m≤10^{18}$

题目背景 - 续

I once swore to be with him forever, I once swore to be with him forever,

and being able to make such a vow made me incredibly ha$p$y.and being able to make such a vow made me incredibly ha$p$y.

I once swore to be with her forever,I once swore to be with her forever,

and being able to make such a vow made me incredibly peaceful.and being able to make such a vow made me incredibly peaceful.

Having such feelings makes me incredibly ha$p$y.Having such feelings makes me incredibly ha$p$y.

Having such feelings makes me incredibly joyful.Having such feelings makes me incredibly joyful.

He once said to me: I will definitely make you ha$p$y.He once said to me: I will definitely make you ha$p$y.

I once said to her: I will definitely make you ha$p$y.I once said to her: I will definitely make you ha$p$y.

Hearing him say that made me incredibly ha$p$y.Hearing him say that made me incredibly ha$p$y.

Being able to say that to her made me incredibly satisfied.Being able to say that to her made me incredibly satisfied.

He shared so much ha$p$iness with me.He shared so much ha$p$iness with me.

I received so much from her, but I…I received so much from her, but I…

So for sure, I am the ha$p$iest girl in the world right now,So for sure, I am the ha$p$iest girl in the world right now,

no matter what others say.

THINK

问题限制条件就是一个隐藏的 斐波那切数列